La determinación de la Pendiente Media de una Cuenca Hidrográfica, es una de las tareas no sólo más laboriosas, sino también más importantes en la realización de cualquier estudio hidrológico, pues esta Pendiente Media controla la velocidad con que se dará la escorrentía superficial en dicha cuenca. Algunos de los parámetros de mayor uso en la Hidrología Superficial, como el Coeficiente de Escorrentía, se fundamentan en la estimación de la cantidad del volumen total de agua precipitada sobre la Cuenca Hidrográfica que se convertirá en caudal superficial, a partir de parámetros diversos, entre los que destaca el valor de su Pendiente Media.
Entre los métodos existentes en la Hidrología Superficial para la determinación de la Pendiente Media de una Cuenca Hidrográfica, está el de las Cuadrículas asociadas a un vector el cual consiste en realizar un “muestreo” de las pendientes en una serie de puntos dentro de los límites de la Cuenca en estudio y, a partir del estudio de distribución de estas pendientes, obtener el valor de Pendiente Media de nuestra Cuenca.
Veamos, paso a paso, la forma de aplicar este método a la cuenca que encontrarás delimitada en este Dibujo.
1Dividir la Cuenca con una serie de líneas horizontales y verticales (conformando una cuadrícula), con una separación constante, de forma tal de obtener por lo menos 50 puntos de intersección de estas línea dentro de ella. Cada uno de estos puntos serán los que conformen parte de la muestra de sitios dentro de la Cuenca Hidrográfica para el cálculo de las respectivas pendientes.

Con la división presentada en la figura, líneas espaciadas a 40 m entre sí, logramos obtener 53 puntos para la aplicación del Método en la determinación de la Pendiente Media de la Cuenca.
2 Determinar la Pendiente en cada uno de los puntos obtenidos previamente, teniendo en cuenta las siguientes situaciones típicas:
- La condición Normal o Frecuente, sobre todo en los puntos hacia el centro del perímetro de la Cuenca bajo estudio, será cuando podemos trazar una línea de apoyo que es perpendicular a la curva de nivel más cercana al punto en cuestión y, al extenderla, se consigue con la siguiente curva de nivel. Por ejemplo, en el punto E4, tenemos lo siguiente:
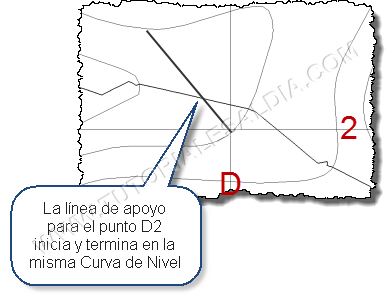
- Una situación especial, es cuando la línea de apoyo no se intercepta en su punto final con una curva de nivel de elevación diferente a la de su punto inicial. Este es el caso del Punto D2:
- Una variante del caso anterior es cuando, aún con interpolación, no se logra que la línea de apoyo esté entre dos curvas de nivel diferentes. En nuestra Cuenca de ejemplo, con el punto A3, tenemos esta situación:
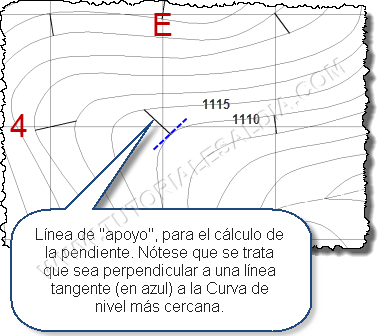
De esta forma, conociendo que la diferencia de elevación entre los extremos de la línea de apoyo es de 5 m (1115-1110 m) y determinando su longitud, 12,94 m, podremos aplicar la ecuación de pendiente (triángulo):

Esto implicaría que el terreno es horizontal (pendiente 0) lo cual, si bien no es una situación imposible, no es del todo cierto en nuestro ejemplo en donde queda claro que el punto está en una ladera de la cuenca (además está cerca de su divisoria).
Para solventar esta situación tenemos que generar, por interpolación, las curvas de nivel necesarias para “rodear” al punto en cuestión:


Es así que, en casos como éste, utilizaremos la pendiente calculada con la curva de nivel inferior a aquella más cercana al punto en cuestión. En este caso utilizamos las cotas 1.195 (la más cercana al punto) y la cota 1190.
Finalmente, habiendo determinado las pendientes para todos los puntos dentro de la Cuenca Hidrográfica en estudio, queda es realizar el análisis de frecuencias para determinar finalmente la Pendiente Media: 3
Con la pendiente de todos los puntos definidos por las cuadrículas, se ordenarán de menor a mayor para agruparlos posteriormente en una cantidad de intervalos de clase (K) definido por la ley de Sturges:

En dónde n es el número de puntos de pendiente (53 en nuestro ejemplo). Si n = 53, K = 7, redondeando por exceso.
Como cada intervalo debe tener un tamaño, utilizaremos la diferencia entre la pendiente máxima y mínima calculada para los puntos y lo dividiremos entre el número de Intervalos de clase:

Con lo que, para nuestra Cuenca de Ejemplo, resulta en:
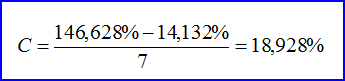
Finalmente, para la determinación de la Pendiente Media de la Cuenca, creamos la siguiente Tabla:
|
Intervalo de Pendientes (%) |
Num. Ocurrencias (N) |
Pendiente Media en el Intervalo Sm (%) |
N x Sm (%) |
|
|
14,13 |
33,06 |
8 |
23,60 |
188,77 |
|
33,06 |
51,99 |
18 |
42,52 |
765,43 |
|
51,99 |
70,92 |
17 |
61,45 |
1.044,68 |
|
70,92 |
89,84 |
7 |
80,38 |
562,66 |
|
89,84 |
108,77 |
1 |
99,31 |
99,31 |
|
108,77 |
127,70 |
1 |
118,24 |
118,24 |
|
127,70 |
146,63 |
1 |
137,16 |
137,16 |
|
Totales |
53 |
2.916,26 |
||
De aquí, la Pendiente Media de la Cuenca Hidrográfica de ejemplo será:

Hidrología en la Ingeniería, Segunda Edición. Germán Monsalve S. Editorial Escuela Colombiana de Ingeniería. Enero 2.002.

EXCELENTE POR FACILITAR LAS HERRAMIENTAS.
MUCHAS GRACIAS